Hypotenuse-Leg (HL) for Right Triangles

Hypotenuse-Leg (HL) for Right Triangles

There is one case where SSA is valid, and that is when the angles are right angles.

Using words:

In words, if the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of a second right triangle, then the triangles are congruent.

Using labels

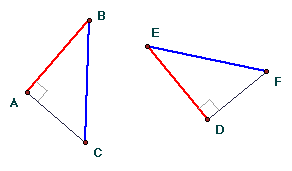
If in triangles ABC and DEF, angle A = angle D = right angle, AB = DE (leg), and BC = EF (hypotenuse), then triangle ABC is congruent to triangle DEF.

Proof:

Begin with two triangles ABC and DEF. In the figure, the known congruent segments are color-coded.

One can construct a point F' on line AC, on the side of A opposite C, so that AF' is congruent to DF. Then triangle ABF' is congruent to triangle DEF by SAS, since AB = DE and angle BAC = angle BAF' = right angle = angle EDF.

But the triangle BF'C is an isosceles triangle, since BF' = EF = BC, and line BA is an altitude. We know from the theory of isosceles triangles that triangle ABC is congruent to triangle ABF'. Since the latter triangle is congruent to triangle DEF, then triangle ABC is congruent to triangle DEF.